At first, we sample ![]() in the
in the ![]() (
(![]() is odd) equidistant points around
is odd) equidistant points around ![]() :
:
![]()
where ![]() is some step. Then we interpolate points
is some step. Then we interpolate points ![]() by polynomial
by polynomial
(1) 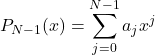
Its coefficients ![]() are found as a solution of system of linear equations:
are found as a solution of system of linear equations:
(2) ![]()
Here are references to existing equations: (1), (2). Here is reference to non-existing equation (??).
![Rendered by QuickLaTeX.com \[ \boxed{f(x)=\int_1^{\infty}\frac{1}{x^2}\,\mathrm{d}x=1} \]](https://api.calculatortimes.com/wp-content/ql-cache/quicklatex.com-356964ca453f1a88657e3ecb6d19a715_l3.png)
![]()
Leave a Reply